Version of June, 2005
This is a rather more extensive complex number library than the one provided in the standard library. It provides complex, imaginary and polar classes and a representation of the i or j of complex analysis. It does not use templates. As in my other libraries, this library is based on a floating point type Real. This must be typedefed to be double, float or a class defined by the user (this is done in the file include.h).
This library is not going to replace the one in the standard library - so use this one only if you need its additional facilities or you really don't want to use the standard one.
As usual with my libraries, there are no restrictions on the use of this library. If you distribute it, you should note that it is available essentially for free on the Internet.
Use is at your own risk. I take no responsibility for errors and problems or losses you may incur through the use of this library. But please report errors.
See the documentation for newmat11 for setting options in the file include.h .
Go to the download page for the library.
Author: Robert Davies; robert at statsresearch.co.nz.
Available from http://www.robertnz.net
The following files are included in this package
| cx.h | header file for the complex number library |
| cx.cpp | function bodies |
| cx_polar.cpp | function bodies for polar class |
| boolean.h | simulation of the standard Boolean type |
| myexcept.h | header for the exceptions simulator |
| myexcept.cpp | bodies for the exceptions simulator |
| include.h | options header file (see documentation in newmat10) |
| cxtest.h | test program header file |
| cxtest.cpp | test program main function |
| cxtest1.cpp | test unary functions |
| cxtest2.cpp | test binary functions |
| cxtest.txt | output from the test program |
| array1.h | simple array class used by test program |
| mandel.cpp | Mandelbrot set example |
| mandel.txt | Output from mandel.cpp |
| cx_targ.txt | target file for use with genmake |
| cx_b55.mak | make file for Borland 5.5 compiler |
| cx_b56.mak | make file for Borland 5.6 compiler |
| cx_m6.mak | make file for VC++ 6, 7 compilers |
| cx_ow.mak | make file for Open Watcom compiler |
| cx_gnu.mak | make file for Gnu compiler |
| cx_cc.mak | make file for CC compiler |
| cx_i8.mak | make file for Intel 8.1 compiler for Windows |
| cx_il8.mak | make file for Intel 8.1 compiler for Linux |
| cx.htm | this file |
| rbd.css | Style sheet for cx.htm |
| polar.gif | diagram of polar coordinates |
| mandel.gif | Mandelbrot set example |
I have tested this program on the Borland 5.5,5.6; MS VC++ 6,7; Gnu 3.3, 3.4; Intel 8. The test program uses templates so you will not be able to run the test program on compilers that don't support templates. I couldn't get the templates in the test program to compile with the Sun CC compiler. The program didn't compile with the Open Watcom (1.3) compiler.
I include make files for the test programs for several compilers - see the file list. Make files for some other compilers can be generated with my genmake utility.
If the program is working correctly the output from the test program will end with two lines similar to
maximum from cxtest1: 3.10082e-14 maximum from cxtest2: 7.10543e-15The exact values will, most likely, differ. These values are from the Borland 5.02 compiler.
For older compilers that don't support bool variables you need to edit include.h to enable my simulated Booleans (comment out the statement #define bool_LIB 0).
You will need to #include files include.h and cx.h in your programs that use this package. Edit include.h to determine whether exceptions are to be used, simulated or disabled. If you use the simulated exceptions you should turn off the exception capability of a compiler that does support exceptions. If you want to use namespace activate the use_namespace definition. This library uses the namespace name RBD_COMPLEX.
| May, 2000 | Initial release |
| July, 2001 | Improve compatibility with my other libraries, include sum_square() function |
| class | description | user |
| class CX | complex | yes |
| class Imag | imaginary | yes |
| class ImaginaryUnit | the i or j of complex analysis | yes |
| class Polar | polar | yes |
| class ConvertFromReal | prevent implicit conversion | no |
| class Quadrant | mod 4 arithmetic | no |
Class CX is the main complex class. I have chosen the name CX so as not to conflict with other complex classes. For example, using complex will clash with the standard library.
Class Imag defines imaginary variables. If you have a complex variable that will always be imaginary (the real part is always zero), then use the Imag class to save computer time and make the program clearer.
Class ImaginaryUnit is used to represent i = sqrt(-1). I use this to define _I_ as a global variable to represent i.
Class Polar represents a complex number in polar coordinates.
I use class ConvertFromReal is used to prevent implicit conversions from Real to Imag. Modern C++ compilers use the keyword explicit to prevent implicit conversion, but, at present I don't want to assume all compilers implement explicit.
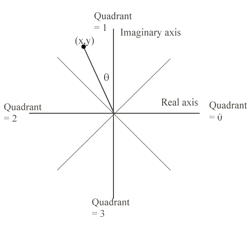
Class Quadrant is used by class Polar in the representation of the angle part of the polar coordinate.
The angle in the polar coordinates is represented by theta which is no greater than pi/4 in absolute value and represents the angle from one of the axes. Quadrant shows which axis. A char value in a Quadrant object can take on one of the values 0, 1, 2 or 3 corresponding to the positive real axis, the positive imaginary axis, the negative real axis or the negative imaginary axis respectively. This representation means that one doesn't lose accuracy when converting from complex coordinates to polar coordinates for complex numbers very close to the real or imaginary axes.

| CX() | constructor, don't set values |
| CX(Real x, Real y) | set real part to x, imaginary part to y |
| CX(Real x) | set real part to x, imaginary part to 0 |
| CX(Imag y) | set real part to 0, imaginary part to y |
| CX(ImaginaryUnit) | set real part to 0, imaginary part to 1 |
| CX(const CX& z) | copy constructor |
| CX(const Polar& p) | convert polar value p to complex |
| Imag() | constructor, don't set values |
| Imag(ConvertFromReal x) | set real part to x. ConvertFromReal stops implicit conversions |
| Imag(const Imag& z) | copy constructor |
| Imag(ImaginaryUnit) | set value to i |
| Polar() | constructor, don't set values |
| Polar(Real r, Real theta) | set polar coordinates to r, theta after normalising |
| Polar(Real x) | set polar coordinates to x, 0 or -x, pi |
| Polar(Imag y) | set polar coordinates to y, pi/2 or -y,-pi/2 |
| Polar(ImaginaryUnit) | set polar coordinates to 1, pi/2 |
| Polar(const CX& z) | convert complex z to polar |
| Polar(const Polar& p) | copy constructor |
| Function | Description | Return types with this class | |||
| CX | Imag | _I_ | Polar | ||
| real() const | real part | Real | Real | Real | |
| real() | ref. to real part | Real& | |||
| imag() const | imaginary part | Real | Real | Real | |
| imag() | ref. to imaginary part | Real& | Real& | ||
| imag_as_imag() const | imaginary part as Imag | Imag | Imag | Imag | |
| conj() const | conjugate | CX | Imag | Polar | |
| cabs() const | absolute value | Real | Real | Real | |
| cabs() | ref. to absolute value | Real& | |||
| arg() const | argument | Real | Real | Real | |
| sum_square() const | square of cabs | Real | Real | Real | |
| operator+() const | + prefix op. | CX | Imag | _I_ | Polar |
| operator-() const | - prefix op. | CX | Imag | Imag | Polar |
| theta() const | theta | Real | |||
| theta() | ref. to theta | Real& | |||
| quadrant() const | quadrant | Quadrant | |||
| quadrant() | ref. to quadrant | Quadrant& | |||
| assert_is_valid() const AssertIsValid() const |
check Polar valid | void | |||
For example:
CX z = 3.0 + 4.0 * _I_; cout << z.real() << ", " << z.imag() << endl;
outputs 3.0, 4.0 .
The declaration of z could have been replaced with any of the following:
CX z(3.0, 4.0); CX z; z.real() = 3.0; z.imag() = 4.0; CX z = 3.0 + Imag(4.0); Polar p(5.0, atan(4.0 / 3.0)); CX z = p;
Note that there are two versions of z.real() and z.imag() for CX variable, z. The non-const version is used when z hasn't been declared as const. This version can be used on the left-hand side of an = sign. The same applies for p.cabs(), p.theta() and p.quadrant() for Polar variable p.
It might seem more natural for z.imag() to return a variable of type Imag rather than Real. However, this would be unusual for those used to the standard library or Fortran. I include another function z.imag_as_imag() which does return the imaginary part as type Imag. Nevertheless, there is a potential source of error, here, if z.imag() is used when z.imag_as_imag() was intended.
sum_square() is the norm function in the standard. It isn't a norm in the mathematical sense so you wouldn't call it norm would you?
assert_is_valid checks that a Polar variable is valid. An exception is thrown if the value is invalid; for example the absolute value of the member variable Theta is greater than pi/4. This should not be possible unless a Polar object is uninitialised or invalid values have been entered with the cabs, theta or quadrant functions.
| Function | Description | Return types with this class | |||
| CX | Imag | _I_ | Polar | ||
| real(.) | real part | Real | Real | Real | |
| imag(.) | imaginary part | Real | Real | Real | |
| imag_as_imag(.) | imaginary part as Imag | Imag | Imag | Imag | |
| conj(.) | conjugate | CX | Imag | Polar | |
| cabs(.) | absolute value | Real | Real | Real | |
| fabs(.) | absolute value | Real | Real | Real | |
| norm1(.) | fabs(real) + fabs(imag) | Real | |||
| arg(.) | argument | Real | Real | Real | |
| exp(.) | exponential | CX | CX | ||
| log(.) | natural log | CX | CX | CX | |
| polar_exp(.) | exponential | Polar | Polar | ||
| sqrt(.) | square root | CX | CX | Polar | |
| square(.) | square | CX | Real | Polar | |
| sum_square(.) | square of cabs | Real | Real | Real | |
| sin(.) | sin trig. function | CX | Imag | ||
| cos(.) | cos trig. function | CX | Real | ||
| tan(.) | tan trig. function | CX | Imag | ||
| sinh(.) | sinh hyperbolic fn. | CX | Imag | ||
| cosh(.) | cosh hyperbolic fn. | CX | Real | ||
| tanh(.) | tanh hyperbolic fn. | CX | Imag | ||
For example:
CX z = 3.0 + 4.0 * _I_; cout << real(z) << ", " << imag(z) << endl;
outputs 3.0, 4.0 .
Only the const versions of real(z) and imag(z) are provided. The comments about the member functions .imag() and .imag_as_imag() also apply here. Note the differences between imag(z), imag_as_imag(z) and Imag(z).
CX z = 3.0 + 4.0 * _I_; Real a = imag(z); // returns a = 4 Imag b = imag_as_imag(z); // returns b = 4i Imag c = Imag(z); // error, can't convert CX to Imag
It is important not to confuse Imag and imag or Real and real.
The functions fabs and cabs are alternative names for the same function.
The function norm1 returns the sum of the absolute values of the real and imaginary parts. This is faster than cabs and may be sufficient for deciding, for example, whether the absolute value of a complex number is less than some bound.
The function polar_exp takes the exp of a complex number and returns the result in polar coordinates.
| =, conversions | To | ||||
| From | CX | Real | Imag | _I_ | Polar |
| CX | Yes | Yes | |||
| Real | Yes | (Yes) | Yes | ||
| Imag | Yes | Yes | Yes | ||
| _I_ | Yes | Yes | Yes | ||
| Polar | Yes | Yes | |||
The only conversions allowed are ones that do not lose information (apart from round-off error). For example, you cannot convert Polar to Imag.
I return void from the = operation so you can't do a = b = c; .
| +, - | Second Argument | ||||
| First Argument | CX | Real | Imag | _I_ | Polar |
| CX | CX | CX | CX | CX | CX |
| Real | CX | (Real) | Imag | Imag | CX |
| Imag | CX | Imag | Imag | Imag | CX |
| _I_ | CX | Imag | Imag | Imag, Real | CX |
| Polar | CX | CX | CX | CX | CX |
When additions or subtractions involve Polar the Polar number is converted to CX and a CX addition or subtraction performed.
| *, / | Second Argument | ||||
| First Argument | CX | Real | Imag | _I_ | Polar |
| CX | CX | CX | CX | CX | illegal |
| Real | CX | (Real) | Imag | Imag | Polar |
| Imag | CX | Imag | Real | Real | Polar |
| _I_ | CX | Imag | Real | Real | Polar |
| Polar | illegal | Polar | Polar | Polar | Polar |
Multiplication of a CX variable with a Polar variable will result in a compile error. Either convert the CX variable to Polar, if you want a Polar result or the Polar variable to CX if you want a CX result.
| +=, -= | Argument | ||||
| Class | CX | Real | Imag | _I_ | Polar |
| CX | Yes | Yes | Yes | Yes | Yes |
| Real | (Yes) | ||||
| Imag | Yes | Yes | |||
| _I_ | |||||
| Polar | Yes | Yes | Yes | Yes | Yes |
| *=, /= | Argument | ||||
| Class | CX | Real | Imag | _I_ | Polar |
| CX | Yes | Yes | Yes | Yes | Yes |
| Real | (Yes) | ||||
| Imag | Yes | ||||
| _I_ | |||||
| Polar | Yes | Yes | Yes | Yes | Yes |
| ==, != | Second Argument | ||||
| First Argument | CX | Real | Imag | _I_ | Polar |
| CX | bool | bool | bool | bool | illegal |
| Real | bool | (bool) | bool | false | bool |
| Imag | bool | bool | bool | bool | bool |
| _I_ | bool | false | bool | true | bool |
| Polar | illegal | bool | bool | bool | bool |
Remember that, because of round-off error, testing equality of floating point variables is not very useful unless the variables involved have values that can be represented exactly as binary numbers or might be equal because one is a copy of the other.
| pow | Second Argument | ||||
| First Argument | CX | Real, int | Imag | _I_ | Polar |
| CX | CX | CX | CX | ||
| Real | CX | (Real) | CX | ||
| Imag | CX | CX | CX | ||
| _I_ | |||||
| Polar | Polar | Polar | Polar | ||
If y is of type int and in the range -12 to 12 then pow(x,y) is calculated by direct multiplication. In all other cases it is calculated with exp(y * log(x)).
Value of pow(x,y) if x is zero:
| x | y | pow(x,y) |
| 0 | int and negative | throw exception |
| 0 | int and non-negative | 0 |
| 0 | not int and non-positive real part | throw exception |
| 0 | not int and positive real part | 0 |
Make sure you understand what you are doing if you use pow(x,y) with complex y.
I have not defined input and output functions.
Real pi, pi_times_2, pi_over_2, pi_over_4 Real ipow(Real x, int n)
ImaginaryUnit _I_
The variables pi, pi_times_2, pi_over_2, pi_over_4 have the obvious values.
The global variable _I_ is the representation of i = sqrt(-1).
The function ipow is pow with integer second argument, n. If n is in the range -12 to 12 the value is calculated by multiplication. An version of pow with integer argument is included in the new standard but is not in all compilers.
The example calculates what is essentially the boundary of the Mandelbrot set using contour integration. Details are given in the program file. The program outputs the coordinates of the points on the boundary. Here is an Excel scatter plot of the points. The program is mostly a demonstration of the CX class but there is a little use of the Imag class and _I_. A copy of the output from the program is in mandel.txt. Your output will probably differ because of the formatting of the output and round-off error.
